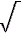


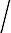
b
7.1 Obecný lineární model
Metody zmíněné v tomto textu mohou být popsány prostřednictvím obecného lineárního modelu (nebo zobecněný lineární model zahrnuje probitovou a logitovou metodu). Nejprve je nutno defmovat lineární strukturální matici X (nebo matici plánu), ve které každý řádek představuje jedno pozorování a každý sloupec lineární efekt (přípravek, blok, sloupec, dávku). Např. plán latinských čtverců z příkladu 5.1.2 je popsán maticí s 36 řádky a 13 sloupci. Jeden sloupec pro každý přípravek, jeden sloupec pro každou dávku, pět sloupců pro každý blok s výjimkou prvního. Všechny sloupce s výjimkou sloupců pro dávky jsou vyplněny čísly 0 nebo 1 podle toho, zda tomuto pozorování odpovídá příslušný efekt. Vektor Y obsahuje (transformované) pozorované hodnoty. Efekty jsou odhadovány vzorcem (X'X)-1X'Y a z nich jako podíl odpovídajících efektů se vypočte odhad účinnosti m. Intervaly spolehlivosti se vypočtou pomocí Fiellerovy věty:
| mL,mU = | 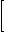 |
m - | gv12 | ± | ts | 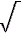 |
v11 - 2mv12 + m2v22 - g |  |
v11 - | v122 |  |
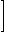 |
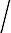 |
(1 - g) , |
| v22 |
b |
v22 |
| kde g = | t2s2v22 |
|
b2 |
a v11, v22 a v12 představují rozptyly čitatele, jmenovatele a jejich kovarianci. Ty se získají přímo z (X'X)-1 nebo nepřímo z var (a1 - a2) = var (a1) + var (a2) - 2 cov (a1, a2) a cov (a1 - a2, b) = cov (a1, b) - cov (a2, b).
Úplná analýza rozptylu, ve které jsou obsaženy všechny komponenty, je poněkud komplikovanější. Matice X by musela být rozšířena o další sloupce, umožňující testovat předpoklad rovnoběžnosti a linearity. Pro zkoušku závisející na kvantální odpovědi se najdou lineární efekty (průsečíky aS, aT atd. a společný sklon b se získá maximalizací součtu n ln Φ(ai + bx) + (n - r)ln(1- Φ(ai + bx)), kde je x logaritmus dávky, Φ představuje tvar rozložení a i ∈ {S, T, ...} .